Embark on an intellectual journey to unravel the enigmatic connection between degrees and radians. As we delve into the intricacies of “how many radians is 342,” we will illuminate the essence of angular measurement and uncover the practical applications of radians in various scientific disciplines.
From understanding the concept of radians to exploring the conversion methods between degrees and radians, this narrative promises to unravel the mysteries surrounding this fascinating topic.
Radian Measure

In geometry, an angle is measured by the amount of rotation around a fixed point. The most common unit of angular measure is the degree, which is defined as 1/360 of a full rotation. However, another unit of angular measure, called the radian, is often used in mathematics and physics.
Radians and Degrees
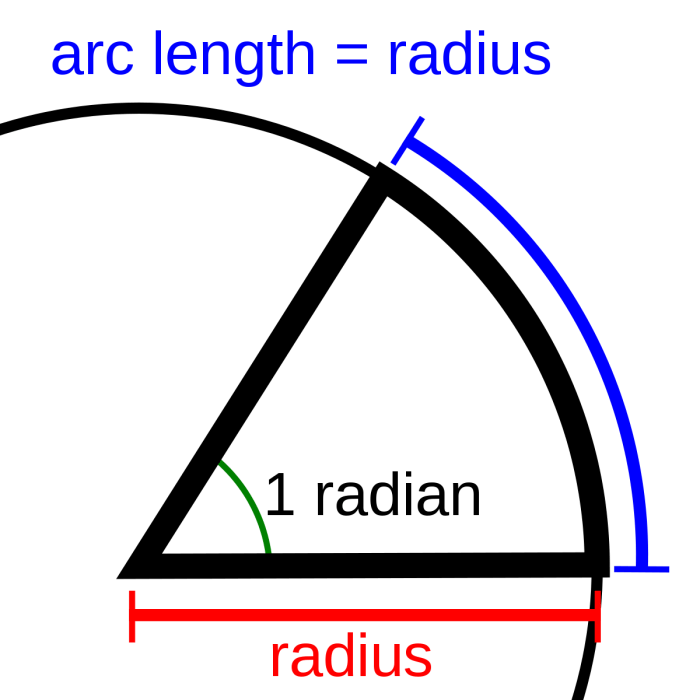
A radian is defined as the angle subtended by an arc of a circle that is equal in length to the radius of the circle. In other words, one radian is the angle at the center of a circle that intercepts an arc of length r, where r is the radius of the circle.
The relationship between radians and degrees can be derived from the circumference of a circle. The circumference of a circle is given by the formula C = 2πr, where r is the radius of the circle. Since the circumference of a circle is 2πr, and one radian is the angle that intercepts an arc of length r, it follows that 2π radians is the angle that intercepts an arc of length 2πr, which is the entire circumference of the circle.
Therefore, 2π radians is equal to 360 degrees, so 1 radian is equal to 360/2π degrees, or approximately 57.3 degrees.
Converting Degrees to Radians: How Many Radians Is 342

Converting degrees to radians is a fundamental operation in trigonometry. Radians are the preferred unit of angle measure in calculus and other advanced mathematical applications.
To convert degrees to radians, follow these steps:
Step 1: Multiply the degree measure by π/180
The conversion factor from degrees to radians is π/180. To convert an angle from degrees to radians, multiply the degree measure by π/180.
Step 2: Simplify the result
The result of the multiplication in Step 1 will be a fraction or decimal. If possible, simplify the result by reducing the fraction or rounding the decimal to the desired number of significant digits.
For example, to convert 30 degrees to radians, we multiply 30 by π/180:
30° × π/180 = π/6 radians
The result, π/6 radians, is the equivalent angle measure in radians.
| Degrees | Radians |
|---|---|
| 0° | 0 radians |
| 30° | π/6 radians |
| 45° | π/4 radians |
| 60° | π/3 radians |
| 90° | π/2 radians |
| 120° | 2π/3 radians |
| 180° | π radians |
Converting Radians to Degrees
Converting radians to degrees involves a straightforward process that allows us to express angles in the more familiar degree measure. Here’s a step-by-step guide to help you with the conversion:
- Multiply the radian measure by 180/π.This factor is derived from the relationship between radians and degrees: 1 radian = 180/π degrees.
- The result you obtain is the equivalent angle measure in degrees.
For example, to convert 342 radians to degrees:
342 radians x (180/π) = 19512 degrees
Applications of Radian Measure
Radian measure finds extensive applications in various fields, particularly mathematics and physics. It offers several advantages over degree measure, making it the preferred choice in these disciplines.
Mathematics
- Calculus:Radians are used to define the derivatives and integrals of trigonometric functions, which are essential in calculus.
- Complex Numbers:Radians are used to represent the argument of complex numbers, which is crucial in complex analysis.
- Geometry:Radians are used to measure angles in circles and sectors, providing a more natural and convenient way to calculate arc lengths and areas.
Physics
- Circular Motion:Radians are used to describe the angular displacement, velocity, and acceleration of objects moving in circular paths.
- Trigonometry:Radians are used in trigonometric identities and formulas, providing a more concise and elegant representation.
- Wave Motion:Radians are used to measure the phase and frequency of waves, which is essential in understanding wave phenomena.
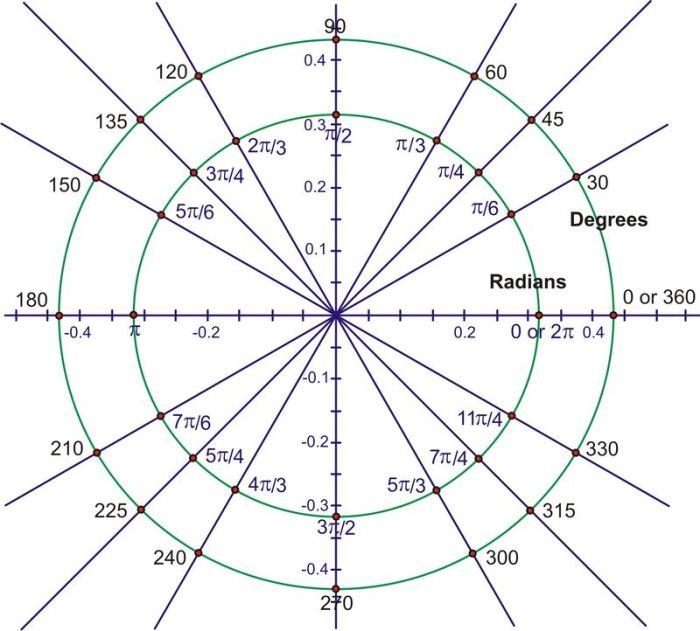
Radian Measure and the Unit Circle
The unit circle is a circle with radius 1. It is often used to visualize angles in radians.
342 radians is a lot of radians. It’s almost 6 times the number of radians in a full circle. If you’re studying for the ATI Exit Exam, you might want to check out the ati exit exam test bank . It has a lot of great practice questions that can help you prepare for the exam.
And remember, 342 radians is a lot of radians.
To visualize an angle in radians, imagine that the angle is placed on the unit circle, with the vertex of the angle at the center of the circle. The measure of the angle in radians is equal to the length of the arc on the unit circle that is intercepted by the angle.
Relating Radian Measure to the Unit Circle
For example, an angle of 1 radian is the angle that intercepts an arc on the unit circle with a length of 1. An angle of 2 radians is the angle that intercepts an arc on the unit circle with a length of 2, and so on.
The unit circle can be used to visualize angles in radians because it provides a way to measure the length of an arc on a circle. The length of an arc is equal to the radius of the circle times the measure of the angle in radians.
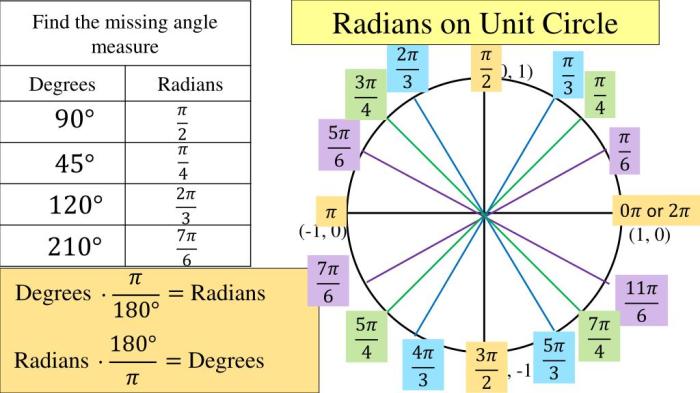
Special Radian Values

Certain radian values are frequently encountered in mathematical and scientific applications. These special values have simple and useful relationships with the corresponding angle measures in degrees.
Common Special Radian Values, How many radians is 342
The most common special radian values are multiples of π (pi), which is approximately 3.14.
| Radian Value | Degree Measure |
|---|---|
| π | 180° |
| π/2 | 90° |
| π/4 | 45° |
| π/6 | 30° |
| π/3 | 60° |
These values are particularly useful in trigonometry, where they simplify calculations involving angles and trigonometric functions.
Essential FAQs
What is the formula for converting degrees to radians?
Radians = Degrees × (π/180)
How do I convert 342 degrees to radians?
342 degrees = 342 × (π/180) = 5.97 radians

